 |
Volume Of Cone
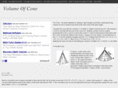
The Cone - the body obtained by rotating a right triangle around line containing the leg. Volume of cone is equal to one-third of the work area of the base height. Consider the cone with the volumes V, of radius R, height h and the top of O. We introduce x-axis to coincide with the axis of the cone-OH. Arbitrary section cone by a plane perpendicular to the x-axis is a circle with center H 1 point of intersection of this plane with the x-axis. Denote the radius of the circle a, r square S (x) by, where x is the abscissa of the H 1. From the similarity triangles and ON 1 A 1 It follows that ON1/ON = R1 / R, or x / h = R1 / R = R1 = XR / h. Since S (x) =? RІ, then S (x) =? RІ / Hi * st Applying the basic formula of calculating the volumes of bodies at a = 0 and b = h, we obtain
Volumeofcone.com ~
Site Info
Whois
Trace Route
RBL Check
|
|
|
|